Spirographs are made of gears.
Gears have teeth or cogs.
Gears can be linear ones...
... or circular arcs.
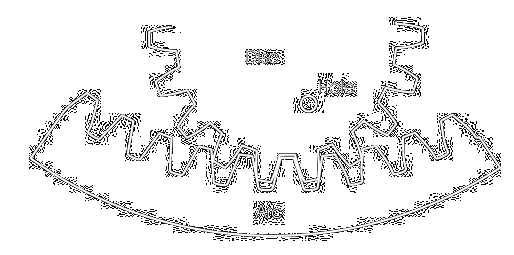
Gears can be assembled together to make a path.
This path always have an integer number of teeth.
There will be another gear, rolling on the path, that we will call disc
The disc have holes.
We can insert a pen in the hole and draw a curve as the disc rolls on the path.
That curve is called spirogram.
The size of a gear can be given by the number of cogs that the gear has.
Computers can compute spirograms, it is not as easy as it seems but it is not too hard either. To describe the path, the disc, the pen and some other parameters of the problem, it is necessary to use a language.
Computer languages are very simple ones, they are very precise and sometimes humans make mistakes when they try to say something with this languages. Computers are selfless, obedient, if humans say something wrong, they just reply: you wrote something wrong, try again.
A program for the spirograph is a text. The text is written in an input dialog in the spirograph web page, the spirograph reads the sentences, and then interprets and executes them.
Let us begin with an example, than can make the concepts clear. Our first goal is create a path.
The pieces of the path are linear gears or arc gears. As we already stated, they have an integer number of teeth and this number will be the size of the gear.
To describe a linear gear we just write L and the number of cogs it has. To describe an arc gear, just write A, the number of cogs it has and the angle of that arc, in degrees.
Positive angles describe arcs turning to the left. Negative angles describe arcs turning to the right. An angle with value cero, describes a line segment, not an arc.
Let us see an example:
|
L 100 A 100 180 L 100 A 100 180 |
You can click on the image above to see the .PDF of the example.
This path is like a stadium track field, it has a linear gear of 100 cogs and then an arc gear of 100 cogs, 180 degrees, then a linear gear of 100 cogs and, finally, an arc gear of 100 cogs, 180 degrees. It has a total of 400 cogs.
NOTE: Remember, we are giving the number of cogs in the arcs, not their radii.
Now, let us roll a disc with 40 cogs on the path assuming we are setting the pen in a hole at the border of the disc.
|
L 100 A 100 180 L 100 A 100 180 D 40 H 40 G |
The G command tells the spirograph: draw a cycle.
The instructions (or commands) do not need to be given one per line. You can also write:
L 100 A 100 180 L 100 A 100 180 D 40 H 40 G
and get the same result.
You can also add comments to explain what you are doing. The spirograph eliminates any text in a line after the sharp sign (#).
L 100 A 100 180 L 100 A 100 180 # stadium track D 40 H 40 # a worker painting funny lanes G
As you can see, the size of the disc is specified by an integer number after the letter D.
The hole is a little more complicated because it is specified by a sequence, although there is no harm is believing that it is a number given after the letter H.
The color of the pen used to draw is given by the C command. As you may know, any color can be expressed as a combination of three rays of light: red, blue, and green. The values for the components are integer number in [0..255].
You may find the next table useful to understand this concept:
| color | name | red | green | blue |
| black | 0 | 0 | 0 | |
| blue | 0 | 0 | 255 | |
| green | 0 | 255 | 0 | |
| cyan | 0 | 255 | 255 | |
| red | 255 | 0 | 0 | |
| magenta | 255 | 0 | 255 | |
| yellow | 255 | 255 | 0 | |
| white | 255 | 255 | 255 | |
| orange | 255 | 165 | 0 | |
| brown | 165 | 42 | 42 | |
| purple | 160 | 32 | 240 | |
| violet | 160 | 32 | 240 |
To set the pen's color to blue, one can write:
|
|
L 100 A 100 180 L 100 A 100 180 D 40 H 40 C 0 0 255 # Blue pen G |
Again, the color must be given by a sequence; by now, we are just giving one color; one color is a sequence.
The T command is used to give the initial direction of the path. Perhaps you have noted that our path has no initial direction. The spirograph supposes that it starts heading to the right. Let us set an initial direction to our path of 60 degrees.
|
T 60 # Initial direction, 60 degrees L 100 A 100 180 L 100 A 100 180 D 60 H 60 C 0 0 255 G T 120 # Initial direction=120 degrees C 0 255 0 # Green G |
Please, note that, in the last example, we have change the disc and the hole. Now we are using a 60 cogs disc and the pen is at the border of this disc. You can also see that the spirograms are not closed. This is because the path's length is not a multiple of the number of cogs of the disc.
Now, when the spirograph rolls the disc, it runs several laps around the path. "N" command sets the number of laps that will be performed per cycle.
|
T 60 L 100 A 100 180 L 100 A 100 180 D 60 H 60 C 0 0 255 N 2 # two laps/cycle G |
If you omit the parameter of the "N" command, the spirograph computes how many cycles you will be required in order to close the spirogram. The number of laps given to (or by) the N command is called a cycle.
|
T 60 L 100 A 100 180 L 100 A 100 180 D 60 H 60 C 0 0 255 N # as many laps as necessary G # to close the spirogram. |
"G" command is used to execute cycles. You can specify how many cycles you want to execute. If you do not give that number, the spiroraph executes only one cycle.
Sometimes the path does not close.
|
L 100 A 100 180 D 60 H 60 N |
|
L 100 A 100 180 D 60 H 60 N G |
But, it is not the same to find the least common multiple of the lengths of the path and the disc than the least common multiple of the CLOSED path and the disc.
The * command will try to close the path. You can use it before computing the numbers of laps per cycle. So, we have:
|
L 100 A 100 180 D 60 H 60 * # close the path C 0 0 255 N G C 0 0 0 E |
We have used command E to show (exhibit) the path. We have used black pen to plot the path the disc and the hole. This command was created for debbuging purposes.
Now let us focus on the disc. If the length of the disc is negative, the disc will lie on the right side of the path.
|
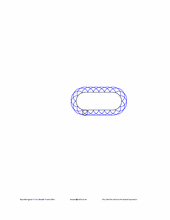
L 100 A 100 180 * D -60 H 60 # disc on the right side of the path C 0 0 255 N G C 0 0 0 E |
Let us draw both the inside and the outside spirogram.
|
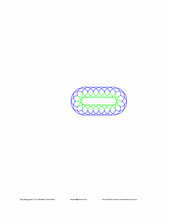
L 100 A 100 180 * C 0 0 255 # outside, blue D -60 H 60 N G C 0 255 0 # inside, green D 60 G |
If you picture a line that is perpendicular to the path, and you put the center of the disc in this line, you will find the hole also in this line, beyond the center of the disc. The disc can be rotated or deviated in its original position with the command V.
|
L 100 A 100 180 * C 0 0 255 D 60 H 60 N E # rotation= 0 C 0 255 0 V 45 E # rotation= 45 C 255 0 0 V 90 E # rotation= 90 |
Now, let us roll the disc...
|
L 100 A 100 180 * C 0 0 255 D 60 H 60 N E # rotation= 0 C 0 255 0 V 45 G # rotation= 45 C 255 0 0 V 90 G # rotation= 90 |
Perhaps you are asking why the angles are taken clockwise if they are positive... Well, it has something to do with the way in which the disc rotates when it rolls on a linear gear. Try to figure out why.
|
?It is a square path with rounded cornersThe hole is changing from the border to the center The colors are changing, gradually, from blue to green and from green to blue. WARNING: If you click the image, prepare yourself to transfer 320 Kilobytes. |
Mmmh... a square path with rounded corners:
|
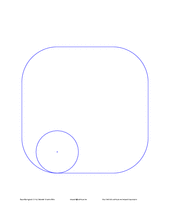
L 200 A 200 90 # a square with rounded corners * X # (closed) centered C 0 0 255 D 480 N |
...but, now, we are going to change at the same time the color, the hole, and the deviation, all at the same time... in 20 steps.
C 0 0 255 H 480 V 0.00 G # step 00 C 0 25 229 H 456 V 4.50 G # step 01 C 0 51 204 H 432 V 9.00 G # step 02 C 0 76 178 H 408 V 13.50 G # step 03 C 0 102 153 H 384 V 18.00 G # step 04 C 0 127 127 H 360 V 22.50 G # step 05 C 0 153 102 H 336 V 27.00 G # step 06 C 0 178 76 H 312 V 31.50 G # step 07 C 0 204 51 H 288 V 36.00 G # step 08 C 0 229 25 H 264 V 40.50 G # step 09 C 0 255 0 H 240 V 45.00 G # step 10 C 0 229 25 H 216 V 49.50 G # step 11 C 0 204 51 H 192 V 54.00 G # step 12 C 0 178 76 H 168 V 58.50 G # step 13 C 0 153 102 H 144 V 63.00 G # step 14 C 0 127 127 H 120 V 67.50 G # step 15 C 0 102 153 H 96 V 72.00 G # step 16 C 0 76 178 H 72 V 76.50 G # step 17 C 0 51 204 H 48 V 81.00 G # step 18 C 0 25 229 H 24 V 85.50 G # step 19 C 0 0 255 H 0 V 90.00 G # step 20
Ok, ok, they are 21 steps... delete the last one.
A computer should do that!
Of course...
/* Quick and Dirty */
#include
int main(void)
{
int k;
for (k=0; k<10; k++)
printf(" C 0 %3d %3d H %3d V %5.2lf G # step %02d\n",
(int)(25.5 * k), (int)(255-25.5*k), 480-k*24, 4.5*k, k);
for (k=10; k<20; k++)
printf(" C 0 %3d %3d H %3d V %5.2lf G # step %02d\n",
(int)(255-25.5*(k-10)), (int)(25.5*(k-10)), 480-k*24, 4.5*k, k);
return 0;
}
|
L 200 A 200 90 # a square with rounded corners * X # (closed) centered D 480 N C 0 0 255 H 480 V 0.00 G # step 00 C 0 25 229 H 456 V 4.50 G # step 01 C 0 51 204 H 432 V 9.00 G # step 02 C 0 76 178 H 408 V 13.50 G # step 03 C 0 102 153 H 384 V 18.00 G # step 04 C 0 127 127 H 360 V 22.50 G # step 05 C 0 153 102 H 336 V 27.00 G # step 06 C 0 178 76 H 312 V 31.50 G # step 07 C 0 204 51 H 288 V 36.00 G # step 08 C 0 229 25 H 264 V 40.50 G # step 09 C 0 255 0 H 240 V 45.00 G # step 10 C 0 229 25 H 216 V 49.50 G # step 11 C 0 204 51 H 192 V 54.00 G # step 12 C 0 178 76 H 168 V 58.50 G # step 13 C 0 153 102 H 144 V 63.00 G # step 14 C 0 127 127 H 120 V 67.50 G # step 15 C 0 102 153 H 96 V 72.00 G # step 16 C 0 76 178 H 72 V 76.50 G # step 17 C 0 51 204 H 48 V 81.00 G # step 18 C 0 25 229 H 24 V 85.50 G # step 19 |
Yes, it works!
argh! we had to make a computer program! it is awful!
A basic sequence is a single value or the description of n ordered data values. It is a n-uple of ordered data.
| The Sequence... | ... means |
a |
a |
a b n |
[a, a+b, a+2b, ... a+(n-1)b] |
| a × n |
[a, a, a, ..., a]
n-times
|
a > b n |
[a, a+h, a+2h, ... a+(n-1)h]
h= (b-a)/n
|
| The Sequence... | ... means |
1 3 5 |
1 4 7 10 13 |
5 -3 4 |
5 2 -1 -4 |
8 × 4 |
8 8 8 8 |
0 > 90 6 |
0 15 30 45 60 75 |
90 > 0 6 |
90 75 60 45 30 15 |
Notes:
a > b ndoes not contain the value b.
Another kind of sequences are the color sequences. They have the same structure than basic sequences but they work on triads of bytes.
If we want to specify a sequence of 10 color values from blue to red, we can write:
0 0 255 > 255 0 0 10
That specifies the colors:
| red | green | blue | color |
| 0 | 0 | 255 | |
| 25 | 0 | 229 | |
| 51 | 0 | 204 | |
| 76 | 0 | 178 | |
| 102 | 0 | 153 | |
| 127 | 0 | 127 | |
| 153 | 0 | 102 | |
| 178 | 0 | 76 | |
| 204 | 0 | 51 | |
| 229 | 0 | 25 |
A sequence is the concatenation of one or more basic sequences separated by a plus sign (+).
Some parameters of the spirograph can be specified by sequences: the pen's color, the hole, the deviation, the initial position, the initial direction; some other, cannot: the disc, the pen's width.
The spirograph works following this algorithm:
In our last example, the parameters could be given as:
|
|
L 200 A 200 90 # a square with rounded corners * X C 0 0 255 D 480 N # colors will change from blue to red gradually, # and back from red to blue using 20 values in between. C 0 0 255 > 0 255 0 10 + 0 255 0 > 0 0 255 10 # holes will change also from 480 to 0 in 20 steps H 480 > 0 20 # and deviations will take their values from 0 to 90 V 0 > 90 20 G 20 |
"There are always possibilities"
Mr. Spock
The spirograph has a lot of more possibilities.
Arcs can have length 0 (zero).
To change the pen's width, use the W width command. In this case, width is a real number with the width of the pen, in points.
To destroy the path use the K command.
To initialize all the sequences, use the Z command.
To change the resolution of the curves, use the R resol command. resol must be an integer number greater than 0.
A scale factor can be introduced with the S scale command. scale must be an real number.
To stop the program, use the command Q. This command was created for debugging purposes.
Any ideas? Do not hesitate in writing me.
Could you believe this?
|
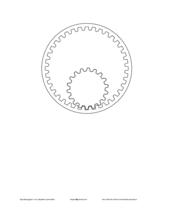
L100A0 85L50A0 -10 L50 A5 -70L50A 5 -70L50A0 -10L50A0 85 * S 0.125 E K P 50 -100 A 8150 360 E K P 110 115 T 5 L70A0 -70L50A0 10 L40 A5 70L50A 5 70L50A0 10L50A0 -70 * E |
I want to thank my beloved wife Norma for her existence itself, because thanks to her patient and loving care, I can create.
I also want to thank my beloved dauthers, Chip & Tut, for being such wonderful girls, because without them, I would have never understood how peaceful are late hours of the night and the early hours of the next day.
Finally, I want to thank to my parents for the spirograph they gave me a long long time ago.
To Norma, with Love,
Eduardo
April 11th, 2005.
e-mail:
